一文梳理 RNN、GRU 和 LSTM

RNN

RNN 的全称是 Recurrent Neural Network，翻译成“循环神经网络”。它是一种用于处理序列数据的神经网络模型。与传统的前馈神经网络不同，RNN 具有向后连接的特性，可以将前面的输出作为后面的输入，从而实现对序列数据的建模和处理。RNN 被广泛应用于自然语言处理、语音识别、机器翻译等领域。一个典型的 RNN 结构图如下：

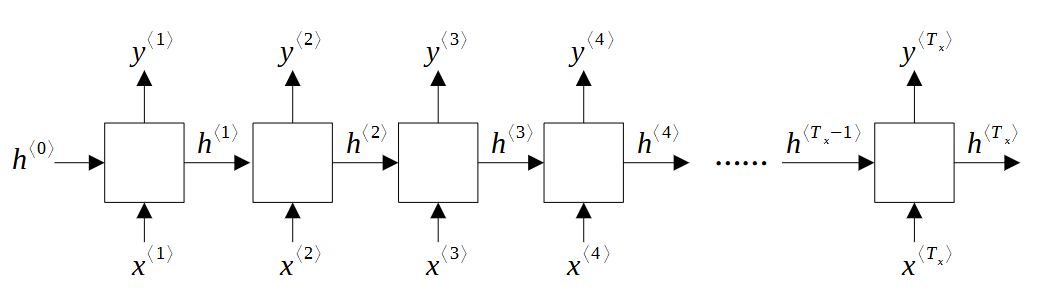
为了统一描述，本文规定：上标 \(\langle t \rangle\) 表示处在时间步第 \(t\) 步的对象或操作。

在这个图中，

• 为了便于说明，我们假设输入和输出具有相同的时间步长，即 \(T_y = T_x\)。

• \(x^{\langle t \rangle}\) 是输入词汇通过 One-Hot 处理后的一维数组，用 \(n_x\) 表示数组大小（它也是词汇表中词汇的数量），也可以用 \(n_x \times 1\) 的矩阵来表示。

• \(y^{\langle t \rangle}\) 是输出的结果。它一般是通过 Sigmoid（二分类）或 Softmax（多元分类）等激活函数处理后的一维数组，用 \(n_y\) 表示数组大小，也可以用 \(n_y \times 1\) 的矩阵来表示。

• \(h^{\langle t \rangle}\) 是隐藏状态 (Hidden State)， \(n_h \times 1\) 矩阵，或大小为 \(n_h\) 的一维数组。每执行一步，其数值都会更新，并把结果传递给下一步。

为什么是这样的结构？没有隐藏状态可以不可以？答案是否定的。如果没有 Hidden State 这个过程媒介，前一次的推理结果不能反馈给下一次推理，相当于所有输入的词汇都没有进行推理而独立生成结果。这显然不符合文本序列的生成规律。

One-Hot 编码处理输入词汇

我们说，\(x^{\langle t \rangle}\) 是 One-Hot 编码后的一维数组，这个数组的长度是词汇表的大小。所谓 One-Hot 编码，是一种将分类变量（在这里是词汇表里定义的各个不同的词汇）转换为数值变量的方法。它将每个分类变量的可能取值映射到一个二进制向量的位置。在这个向量中，只有对应于该分类变量取值的位置为 1，其他位置为 0。

为了简化说明，假设词汇表只有 3 个词汇，分别是 ["a", "b", "c"]，那么词汇 "a" 的索引值是 0，One-Hot 后变成数组 [1, 0, 0]； "b" 的索引值是 1，One-Hot 后变成数组 [0, 1, 0]。依此类推，"c" 用数组 [0, 0, 1]来表示。

实际的词汇表可能长这样：["a", "aaron", ..., "and", ..., "harry", ..., "potter", ..., "zulu"]。更复杂的，还要处理词汇大小写问题（比如处理 green 和 Green），不认识的词汇（比如用 <UNK> 表示），生成结束的标识（比如用 <EOS> 表示），掩码标识（比如用 <MASK> 表示），等等。这些就涉及到分词 (Tokenization) 领域了，本文不做展开。

One-Hot 的好处是将不可计算的分类变量变成了可计算的数组，以便将分类变量输入到模型中进行训练和预测。

Softmax 函数输出概率分布

那么输出的 \(y^{\langle t \rangle}\) 是什么呢？这个取决于不同的应用场合。假如我们希望得到每个词汇被选中的概率，那么 \(n_y\) 就有可能等于 \(n_x\)（当然，有些情况两者也不相等。比如词汇表的末尾几个词汇是特殊 Token，那么 \(y\) 就可能直接去掉它们，从而使得 \(n_y < n_x\)）。

现在就假设 \(n_y = n_x = n\)，即词汇表中有 \(n\) 个词汇，我们希望：

• 输出的 \(y^{\langle t \rangle}\) 是一个长度为 \(n\) 的数组。

• 数组中的每个元素的索引值是对应词汇的索引值，而索引值对应的数值是该词汇被选中的概率，每个值得取值范围是 [0, 1] 。

• 所有元素的数值加起来等于 1。

例如，在上面 ["a", "b", "c"] 的例子中，若输出的结果是 [0.14, 0.08, 0.78]，那么就意味着 "a" 被选中的概率是 0.14，"b"被选中的概率是 0.08，"c" 被选中的概率是 0.78。数组只告诉了我们每个词汇被选中的概率，还不是我们的最终想要输出的词汇，因此还需要进一步处理。例如，可以根据概率随机选择。以下是使用 numpy库随机选择的例子：

import numpy as np

# 词汇表
vocab = ["a", "b", "c"]

# 概率数组
probabilities = [0.14, 0.08, 0.78]

# 词汇表长度
vocab_size = len(vocab) 

# 按照概率输出选中词汇的索引值
index = np.random.choice(vocab_size, p=probabilities) 

# 输出词汇
word = vocab[index]

在深度学习中，通常可以用 Softmax 函数作为输出层的激活函数，将输出值映射到 [0, 1] 之间，同时满足所有输出值之和为 1，表示每个类别的概率，用于判断样本属于那个类别的概率。

Softmax 函数的公式如下所示：

\[ \operatorname{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{n}e^{z_j}} \]

其中，\(z_i\) 是输入向量的第 \(i\) 个分量，\(n\) 是向量的维度。Softmax 函数将输入向量中的每个分量映射到 \([0, 1]\) 区间内，并且所有分量的和为 \(1\)，因此可以将其解释为概率分布。

我曾经尝试询问 ChatGPT，为什么 Softmax 函数需要 e 指数。以下是它的回答，仅供参考：

在 Softmax 函数中，使用 e 指数是因为它具有以下两个性质：

• e 指数是一个正数，它可以保证 Softmax 函数的输出也是一个正数。
• e 指数具有快速增长的特点，这可以使得输出向量中的某些元素比其他元素更突出。

因此，使用 e 指数可以将输入向量中的每个元素转化为一个正数，并且可以突出某些元素的重要性，从而更好地表达输入向量的特征。同时，使用 e 指数也可以使 Softmax 函数具有平滑性和可微性，使得神经网络的训练更加稳定和高效。

定义隐藏状态 (Hidden State)

隐藏状态的维度实质上是定义了 \(n_h\) 个可以在状态之间进行推理传递的独立特征。我们并不清楚这些特征是什么，也不知道总共应该有多少个这样的独立特征。我们能做的，就是假设有 \(n_h\) 个独立特征，然后让机器来学习拟合这些特征。当然，一般来说，\(n_h\)、\(n_x\) 和 \(n_y\) 之间没有直接关系。

前向传播

结合上面的信息，我们可以推断隐藏状态的更新计算方式如下： \[ h^{\langle t \rangle} = \operatorname{g}(W_{hh}h^{\langle t-1 \rangle} + W_{hx}x^{\langle t \rangle} + b_h) \] 其中，

• \(\operatorname{g}\) 是激活函数，可以选择 \(\operatorname{tanh}(\cdot)\), \(\operatorname{relu}(\cdot)\) 等。例如，如果选择的是\(\operatorname{tanh}(\cdot)\)，上面公式就变成：

\[ h^{\langle t \rangle} = \operatorname{tanh}(W_{hh}h^{\langle t-1 \rangle} + W_{hx}x^{\langle t \rangle} + b_h) \]

• 参数矩阵 \(W_{hh}\) 的维度是 \((n_h, n_h)\), 而 \(W_{hx}\) 的维度是 \((n_h, n_x)\)。
• 偏置矩阵 \(b_h\) 的维度和隐藏状态 \(h^{\langle t \rangle}\) 的维度一致，是 \((n_h, 1)\)。

然后用输出的隐藏状态来计算预测值 (Prediction) \(\hat{y}\)： \[ \hat{y}^{\langle t \rangle} = \operatorname{softmax}(W_{yh}h^{\langle t \rangle} + b_y) \] 其中，

• 我们使用 \(\hat{y}\) 表示预测值，而不是标定值。
• 参数矩阵 \(W_{yh}\) 的维度是 \((n_y, n_h)\)。
• 偏置矩阵 \(b_y\) 的维度和预测值 \(\hat{y}^{\langle t \rangle}\) 的维度一致，是 \((n_y, 1)\)。

把这两个公式结合起来，就可以得到如下 RNN 单元的内部结构：

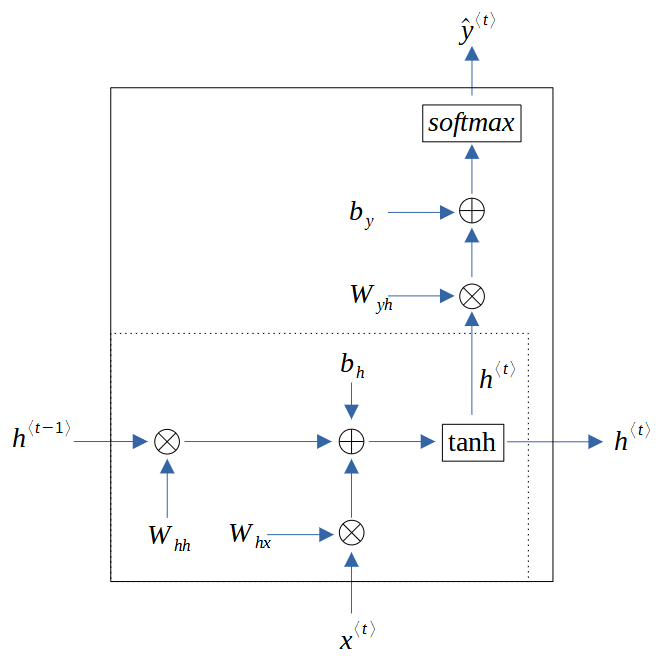
我们也可以借助 NumPy 库，来实现前向传播：

import numpy as np

# 定义 Softmax 激活函数
def softmax(z):
    exp_z = np.exp(z)
    return exp_z / np.sum(exp_z)

# 定义 RNN 类
class RNN:
    def __init__(self, input_size, hidden_size, output_size):
        # 初始化权重和偏置
        self.Whx = np.random.randn(hidden_size, input_size) * 0.01
        self.Whh = np.random.randn(hidden_size, hidden_size) * 0.01
        self.Wyh = np.random.randn(output_size, hidden_size) * 0.01
        self.bh = np.zeros((hidden_size, 1))
        self.by = np.zeros((output_size, 1))
        
    def forward(self, x):
        # 初始化隐藏状态和输出
        h = np.zeros((self.Whh.shape[0], 1))
        y = np.zeros((self.Wyh.shape[0], 1))
        
        # 遍历输入序列
        for t in range(len(x)):
            # 计算隐藏状态
            h = np.tanh(np.dot(self.Whx, x[t]) + np.dot(self.Whh, h) + self.bh)
            # 计算输出
            y = softmax(np.dot(self.Why, h) + self.by)
        
        return y

GRU

从前面 RNN 的结构来看，hidden state 携带的特征信息有助于下一步的推导，因此具备一定的记忆能力。记忆是序列生成的一项重要能力。试想一下，如果你在说一段话的时候，说着说着就不记得前面说了什么，那么后面说的内容可能就与上文没有任何关系，表现出来的就是在胡说八道。那么，传统 RNN 结构的 hidden state 到底能携带多少记忆信息呢？直接增大 hidden state 的维度，携带的记忆信息是否更多？这些可以在实验过程中去尝试。但总的来说，根据以往的经验，随着时间步的增加，这种结构的 RNN 可能会出现梯度消失 (Vanishing gradients) 或梯度爆炸 (Exploding gradients) 的问题。因此，我们也需要根据具体的任务和数据情况，来改进 RNN 架构。GRU 和 LSTM 就是其中的两种。从历史来看，LSTM 比 GRU 更早提出来；但考虑到 GRU 更简单一些，我们就先讨论 GRU。

GRU 是 Gated Recurrent Unit 的简称，由 Cho 等人在 2014 年^[1]提出。与传统的 RNN 相比，GRU 可以更好地处理梯度消失和梯度爆炸等问题，同时也具有更强的记忆能力和表达能力。

GRU 与传统 RNN 相比，增加了一个门控机制，用于控制 hidden state 中的信息流动和遗忘。具体来说，GRU 通过引入更新门和重置门，来控制 hidden state 中的信息更新和遗忘。

• 更新门 (update gate) 用于控制当前时刻输入和上一时刻 hidden state 的“信息更新”。
• 重置门 (reset gate) 用于控制当前时刻输入和上一时刻 hidden state 的“信息遗忘”。

通过这种方式，GRU 可以更好地控制 hidden state 中的信息流动，从而提高模型的性能和记忆能力。

首先，通过 sigmoid 激活函数，定义两个控制门，分别是更新门 \(\Gamma_u^{\langle t \rangle}\) 和 重置门 \(\Gamma_r^{\langle t \rangle}\)： \[ \Gamma_u^{\langle t \rangle} = \sigma(W_{uh}h^{\langle t-1 \rangle} + W_{ux}x^{\langle t \rangle} + b_u) \]

\[ \Gamma_r^{\langle t \rangle} = \sigma(W_{rh}h^{\langle t-1 \rangle} + W_{rx}x^{\langle t \rangle} + b_r) \]

将重置门引入 hidden state，来控制 hidden state 的各个特征是否要重置，如下： \[ \tilde{h}^{\langle t \rangle} = \operatorname{tanh}(W_{hh}(\Gamma_r^{\langle t \rangle} \odot h^{\langle t-1 \rangle}) + W_{hx}x^{\langle t \rangle} + b_h) \] 其中 \(\odot\) 表示逐元素相乘。和前面 hidden state 的更新公式相比，我们用 \(\Gamma_r^{\langle t \rangle} \odot h^{\langle t-1 \rangle}\) 来替换 \(h^{\langle t-1 \rangle}\)。这样做带来的好处是：如果 \(\Gamma_r^{\langle t \rangle}\) 的某个元素是 0，则代表其对应的特征被重置为 0，也就是被遗忘了。另外，我们用 \(\tilde{h}^{\langle t \rangle}\) 而不是 \(h^{\langle t \rangle}\) 来表示输出的结果，是因为它还不是最终的 hidden state，而是 candidate hidden state（候选隐藏状态）。最终的 hidden state 应该是： \[ h^{\langle t \rangle} = (1-\Gamma_u^{\langle t \rangle}) \odot h^{\langle t-1 \rangle} + \Gamma_u^{\langle t \rangle} \odot \tilde{h}^{\langle t \rangle} \] 它通过更新门 \(\Gamma_u^{\langle t \rangle}\) 来控制是否更新到 candidate hidden state 对应的特征。如果 \(\Gamma_u^{\langle t \rangle}\) 的某个元素为 0，那么 \(h^{\langle t-1 \rangle}\) 对应元素的特征值就保留下来了，即不更新；如果为 1，那么就要完全用 \(\tilde{h}^{\langle t-1 \rangle}\) 对应元素的特征值，即完全更新。

LSTM

LSTM 是 Long Short-Term Memory 的简称，是 Hochireiter 和 Schmidhuber 于 1997 年提出的^[2]，比 GRU 早得多。同样为了更好地控制信息流动，LSTM 也拥有门控逻辑。具体来说，LSTM 使用了三个控制门，分别是：

• 输入门 (input gate) \(\Gamma_i\)
• 遗忘门 (forget gate) \(\Gamma_f\)
• 输出门 (output gate) \(\Gamma_o\)

和 GRU 里对门的定义类似，这三个门的公式分别是： \[ \Gamma_i^{\langle t \rangle} = \sigma(W_{ih}h^{\langle t-1 \rangle} + W_{ix}x^{\langle t \rangle} + b_i) \]

\[ \Gamma_f^{\langle t \rangle} = \sigma(W_{fh}h^{\langle t-1 \rangle} + W_{fx}x^{\langle t \rangle} + b_f) \]

\[ \Gamma_o^{\langle t \rangle} = \sigma(W_{oh}h^{\langle t-1 \rangle} + W_{ox}x^{\langle t \rangle} + b_o) \]

现在我们要多引入一个名为 cell state（单元状态，也被称为记忆细胞状态，memory cell state）的项来存储一部分记忆信息，记为 \(c^{\langle t \rangle}\)。和 GRU 的候选隐藏状态类似，cell state 也有它的候选 (candidate) 形式 \(\tilde{c}^{\langle t \rangle}\)，如下： \[ \tilde{c}^{\langle t \rangle} = \tanh(W_{ch}h^{\langle t-1 \rangle} + W_{cx}x^{\langle t \rangle} + b_c) \] 和 GRU 中候选隐藏状态 (candidate hidden state) 不同的是，上述这个操作没有没有引入新的门控。最终的 cell state 如下： \[ c^{\langle t \rangle} = \Gamma_f^{\langle t \rangle} \odot c^{\langle t-1 \rangle} + \Gamma_i^{\langle t \rangle} \odot \tilde{c}^{\langle t \rangle} \] 可以看到，遗忘门 \(\Gamma_f\) 控制前一个状态 \(c^{\langle t-1 \rangle}\) 的遗忘量，输入门 \(\Gamma_i\) 则控制当前新输入状态 \(\tilde{c}^{\langle t \rangle}\) 的输入量。

最后是 hidden state。有了 cell state，我们再通过输出门控制输出量，让 hidden state 用 cell state 来表示： \[ h^{\langle t \rangle} = \Gamma_o \odot \operatorname{tanh}(c^{\langle t \rangle}) \] 仔细对比 GRU 和 LSTM 的形式，你会发现：GRU 是将具有记忆功能的 cell state，直接等价于 hidden state；而 LSTM 则是将两者分离开来。

LSTM 和 GRU 优缺点对比

LSTM 的优缺点

优点

• LSTM 具有记忆单元，能够有效地处理长序列数据，避免了梯度消失或梯度爆炸的问题。
• LSTM 的门控机制可以有效地控制信息流的进出，从而增强了模型的泛化能力。
• LSTM 可以处理多种类型的输入，如文本、音频和图像等。

缺点

• LSTM 的计算复杂度较高，训练时间较长。
• LSTM 的模型结构较为复杂，不易理解和调试。
• LSTM 对于输入序列的长度敏感，需要对序列进行截断或填充。

GRU 的优缺点

优点

• GRU 的计算复杂度较低，训练时间较短。
• GRU 的模型结构较简单，易于理解和调试。
• GRU 的门控机制比 LSTM 更简单，但仍能够有效地控制信息流的进出。

缺点

• GRU 的记忆单元较为简单，可能无法处理特别长的序列数据。
• GRU 的泛化能力可能不如 LSTM。
• GRU 对于输入序列的长度也比较敏感，需要对序列进行截断或填充。

参考

1. Kyunghyun Cho, Bart van Merrienboer, Caglar Gulcehre, Dzmitry Bahdanau, Fethi Bougares, Holger Schwenk, Yoshua Bengio. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. arXiv preprint arXiv: 1406.1078, 2014. ↩︎
2. S. Hochreiter and J. Schmidhuber. 1997. Long short-term memory. Neural Computation, 9(8):1735–1780. ↩︎